Let \(A \in \reals^{n \times n}\) (symmetric) be the adjacency matrix of an undirected graph, so that \(a_{ij}\) is the weight of the edge between nodes \(i\) and \(j\). The degree matrix \(D = \diag(A\mathbf{1})\) is diagonal, such that \(d_{ii} = \sum_{j = 1}^n a_{ij}\) is the (weighted) degree of node \(i\). The Laplacian of this graph is the symmetric matrix \[ L = D - A. \] Simple calculations reveal that \(L\) encodes a neat quadratic form, namely, \[ x^\top L x = \frac{1}{2} \sum_{i,j} a_{ij} (x_i - x_j)^2, \] where the double sum is for \(i\) and \(j\) both ranging from \(1\) to \(n\).
From that expression, it is clear that if the weights \(a_{ij}\) for \(i \neq j\) are nonnegative then \(L\) is positive semidefinite. However, it can happen that \(L\) is positive semidefinite even in the presence of some negative weights. For example, let
\[ A = \begin{bmatrix} 0 & 1 & -\frac{1}{4} \\ 1 & 0 & 1 \\ -\frac{1}{4} & 1 & 0 \end{bmatrix}. \]
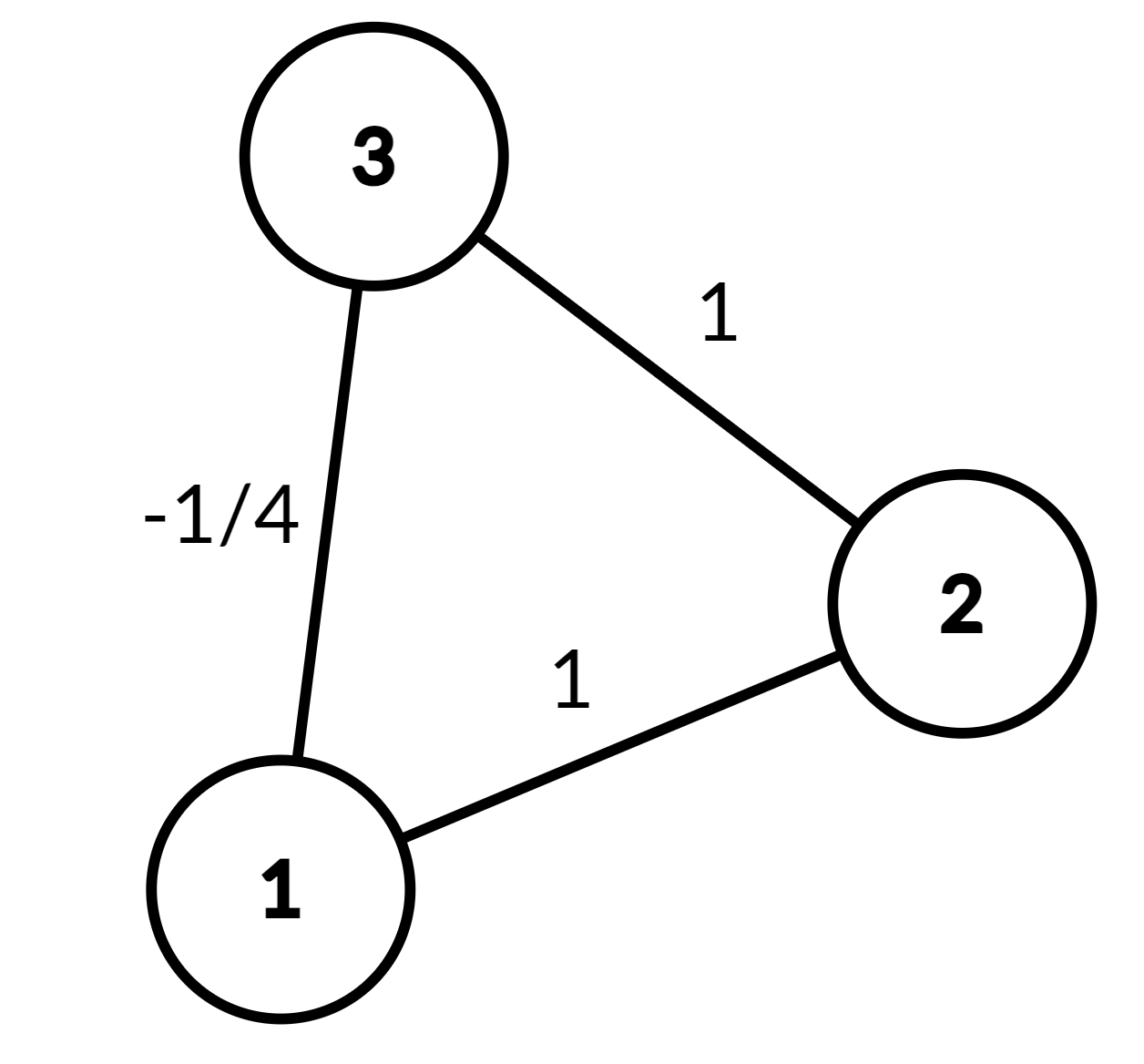
The associated Laplacian is positive semidefinite:
>> A = [0 1 -.25 ; 1 0 1 ; -.25 1 0];
>> D = diag(A*ones(3,1));
>> L = D-A;
>> eig(L)'
ans =
0.0000 0.5000 3.0000
>> We can’t push this too far though: certainly, if all edges are nonpositive, then \(L\) is negative semidefinite.
Thus, it is natural to ask:
If \(L\) is positive semidefinite, what does this reveal about the sign pattern of the edge weights?
Unfortunately, not much. For a connected1 graph, the answer is:
The edges with positive weights form a connected graph.
That is, the set of positive edges includes a spanning tree over the \(n\) nodes. This only forces \(n-1\) edges to have positive weight. And indeed, we can’t deduce more than that in general:
If the edges with positive weights form a connected graph, then all other edges can be negative (as long as they are not too far from zero).
Let us argue the first part with a standard “cut” argument—I saw this recently in an excellent paper by Geshkovski et al. (2024), see their equation (C.3) in arXiv v3. For any nonempty subset \(S \subset \{1, \ldots, n\}\), let \(x \in \reals^n\) be the indicator vector for \(S\), that is, \(x_i = 1\) if \(i \in S\) and \(x_i = 0\) if \(i \notin S\). Then, \(L \succeq 0\) provides \[ 0 \leq x^\top L x = \frac{1}{2} \sum_{i,j} a_{ij} (x_i - x_j)^2 = \sum_{i \in S, j \notin S} a_{ij}. \] (The set \(S\) defines a cut, and the sum on the right-hand side is the cut weight.) Since we assume the graph is connected, at least one of the weights \(a_{ij}\) in that sum is nonzero (otherwise \(S\) and its complement would be disconnected from one another). And since the sum is nonnegative, at least one of the weights is positive. Thus, regardless of how you split the nodes in two clusters (\(S\) and its complement), there must be at least one positive edge going across. In turn, this means that even if we keep only the positive edges, the graph is still connected.
The other way around, the presence of such a spanning tree is sufficient to allow \(L\) to be positive semidefinite. Indeed, start by creating a spanning tree of positive weights. The Laplacian \(L_0\) of that graph has the usual zero eigenvalue (corresponding to the eigenvector \(\mathbf{1}\)), and all other eigenvalues are strictly positive since the graph is connected. Now make any number of the other possible edges have weight \(-\varepsilon < 0\). The resulting Laplacian \(L_\varepsilon\) is a perturbation of \(L_0\): the all-ones vector is still in its kernel so that the zero eigenvalue stays fixed; and we can certainly choose \(\varepsilon\) small enough to ensure that the positive eigenvalues remain positive (by continuity of eigenvalues). Therefore, the new graph is connected, its Laplacian \(L_\varepsilon\) is positive semidefinite, and yet it only has \(n-1\) positive edge weights: all others are negative.
Why might we care? The context in the paper by Geshkovski et al. (2024) is as follows. We have an optimization problem over \(n\) points. The cost function is structured by a graph over these \(n\) points (loosely speaking). The Hessian of the cost function is the Laplacian of that graph, with weights that depend on where the \(n\) points are placed. The weights (in particular, their sign) may reveal something useful about how the points are distributed. This is pretty common (e.g., in synchronization problems, Kuramoto oscillator networks, rotation estimation, opinion dynamics, graph clustering etc.) At second-order critical points, we know that the Hessian is positive semidefinite. Then, we might want to know: what does that reveal about the signs of the weights? Unfortunately, in and of itself, the fact that the Laplacian is positive semidefinite does not tell us that very many weights are positive.
References
Footnotes
The edge between nodes \(i\) and \(j\) is present if \(a_{ij} \neq 0\). We judge connectivity of the graph based on the edges that are present, ignoring the (nonzero) weight on them. If the graph is not connected, you can apply the same reasoning to each connected component separately.↩︎