The difference-of-Hadamard lift of the 1-norm regularizer enjoys \(2 \Rightarrow 1\)

Consider the problem of minimizing a \(C^2\) function \(f \colon \Rn \to \reals\) with a 1-norm regularizer: \[ f_\lambda(x) = f(x) + \lambda \|x\|_1. \qquad(1)\] The larger \(\lambda > 0\), the more the 1-norm promotes sparse solutions. Notice that if \(f\) is convex, then so is \(f_\lambda\).

The cost function \(f_\lambda\) is nonsmooth because of that regularizer. Conveniently, there are several nice ways to smooth it out without changing the problem, as reviewed in (Kolb et al. 2023). In particular, consider the difference-of-Hadamard lift \(\varphi \colon \Rn \times \Rn \to \Rn\) defined as follows, where \(\odot\) denotes entry-wise product: \[ \varphi(y, z) = y \odot y - z \odot z. \qquad(2)\] This has the relevant property that \[ \|x\|_1 = \min_{y,z : \varphi(y, z) = x} \|y\|^2 + \|z\|^2, \qquad(3)\] where \(\|u\| := \sqrt{u^\top u}\) denotes the 2-norm. (To see this, first observe that the problem separates over the \(n\) coordinates, then check that the minimal value of \(y_i^2 + z_i^2\) subject to \(x_i = y_i^2 - z_i^2\) is precisely \(|x_i|\). Indeed, the constraint defines a hyperbola, so by considering the two possible signs of \(x_i\), one can see that the minimum is attained at \((\pm\sqrt{x_i}, 0)\) if \(x_i \geq 0\) or at \((0, \pm\sqrt{-x_i})\) if \(x_i \leq 0\).)

Thus, for the purpose of minimization, at the expense of doubling the number of variables (from \(x\) to \((y, z)\)), we may replace the nonsmooth 1-norm with a smooth sum of squared 2-norms. This yields the following cost function: \[ g_\lambda(y, z) = f(y \odot y - z \odot z) + \lambda(\|y\|^2 + \|z\|^2). \qquad(4)\] Even if \(f\) is convex, there is no reason that \(g_\lambda\) should be convex. Still, the landscape of \(g_\lambda\) is not that bad. This blog post proves the following:

Theorem 1 (\(2 \Rightarrow 1\) for 1-norm regularization.) Fix \(\lambda > 0\) and a \(C^2\) function \(f \colon \Rn \to \reals\). Define \(f_\lambda \colon \Rn \to \reals\) and \(g_\lambda \colon \Rn \times \Rn \to \reals\) as in Eq. 1 and Eq. 4, related by the lift \(\varphi\) in Eq. 2.

If \((y, z) \in \Rn \times \Rn\) is second-order critical for \(g_\lambda\), then \(x := \varphi(y, z)\) is first-order stationary for \(f_\lambda\).

In particular, if \(f\) is convex, then the second-order critical points of \(g_\lambda\) are global minima (benign non-convexity), and \(\varphi\) maps them to the global minima of \(f_\lambda\).

This fact is of the same nature as that described in a previous post about the nuclear norm regularizer. It also falls within the general study of optimization landscapes related by a lift: see (Levin, Kileel, and Boumal 2024).

Optimality conditions

The local and global minima of \(f_\lambda\) are stationary, meaning the subgradient of \(f_\lambda\) contains the zero vector. This condition is easily made explicit in terms of the gradient of \(f\) by using the known expression for the subgradient of the 1-norm, as follows.

Lemma 1 A point \(x\) is stationary for \(f_\lambda\) if and only if for each coordinate \(i \in \{1, \ldots, n\}\) the following hold:

• If \(x_i > 0\), then \(\nabla f(x)_i = -\lambda\),
• If \(x_i = 0\), then \(\nabla f(x)_i \in [-\lambda, \lambda]\), and
• If \(x_i < 0\), then \(\nabla f(x)_i = \lambda\).

Proof. This follows from the stationarity condition \(-\nabla f(x) \in \lambda \partial \|x\|_1\), and the standard expression \[ \partial \|x\|_1 = \{ g \in \Rn : \|g\|_\infty \leq 1 \textrm{ and } g^\top x = \|x\|_1 \}, \] which effectively states that \(g\) is a subgradient of the 1-norm at \(x\) if and only if \(g_i \in \sign(x_i)\), where by convention \(\sign(0) = [-1, 1]\).

Since \(g_\lambda\) is twice differentiable, its local and global minima satisfy first- and second-order necessary optimality conditions, namely, the gradient is zero and the Hessian is positive semidefinite. Simple calculations reveal that these are equivalent to the conditions stated below in terms of \(f\) and \(\lambda\).

In the computations below, with the usual inner product \(\inner{u}{v} = u^\top v\) on \(\Rn\), we repeatedly use that \(\inner{u}{v \odot w} = \inner{u \odot w}{v}\).

Lemma 2 (Second-order critical points of \(g_\lambda\)) A point \((y, z)\) is first-order critical for \(g_\lambda\) if and only if \[\begin{align*} \nabla f(x) \odot y = -\lambda y && \textrm{ and } && \nabla f(x) \odot z = \lambda z, \end{align*}\] where \(x = \varphi(y, z)\). Such a point is also second-order critical if and only if \[ \frac{1}{2} \inner{\dot x}{\nabla^2 f(x)[\dot x]} + \inner{\nabla f(x)}{\dot y \odot \dot y - \dot z \odot \dot z} + \lambda\big(\|\dot y\|^2 + \|\dot z\|^2\big) \geq 0 \] for all \((\dot y, \dot z)\) in \(\Rn \times \Rn\), where \(\dot x = \D\varphi(y, z)[\dot y, \dot z]\).

Proof. The directional derivative of \(g_\lambda\) (Eq. 4) at \((y, z)\) along \((\dot y, \dot z)\) is as follows, with \(x = y \odot y - z \odot z\) and \(\dot x = 2 y \odot \dot y - 2 z \odot \dot z\): \[\begin{align*} \D g_\lambda(y, z)[\dot y, \dot z] & = \D f(x)[\dot x] + 2\lambda( \innersmall{y}{\dot y} + \innersmall{z}{\dot z} ) \\ & = 2\innersmall{\nabla f(x)}{y \odot \dot y - z \odot \dot z} + 2\lambda( \innersmall{y}{\dot y} + \innersmall{z}{\dot z} ). \end{align*}\] From there, it easily follows that the gradient of \(g_\lambda\) is \[ \nabla g_\lambda(y, z) = 2 \Big( \nabla f(x) \odot y + \lambda y, -\nabla f(x) \odot z + \lambda z \Big). \] The first-order conditions require this gradient to be zero. Differentiating the gradient, we get an expression for the Hessian of \(g_\lambda\): \[\begin{align*} \frac{1}{2}\nabla^2 g_\lambda(y, z)[\dot y, \dot z] = \Big( & \phantom{-}\ \nabla^2 f(x)[\dot x] \odot y + \nabla f(x) \odot \dot y + \lambda \dot y, \\ & -\nabla^2 f(x)[\dot x] \odot z - \nabla f(x) \odot \dot z + \lambda \dot z \Big). \end{align*}\] The second-order conditions require this Hessian to be positive semidefinite, that is, \(\inner{(\dot y, \dot z)}{\nabla^2 g_\lambda(y, z)[\dot y, \dot z]} \geq 0\) for all \((\dot y, \dot z)\).

Proof of the theorem

To prove Theorem 1, we assume \((y, z)\) satisfies the conditions provided by Lemma 2 and we aim to verify the conditions required by Lemma 1.

For ease of notation, let \(q = \nabla f(x)\). The first-order conditions provide: \[\begin{align*} q \odot y = -\lambda y && \textrm{ and } && q \odot z = \lambda z. \end{align*}\] Entrywise multiply the first equality by \(z\) and the second by \(y\), then compare them to deduce that \(-\lambda y \odot z = \lambda z \odot y\). Since \(\lambda\) is strictly positive, it follows that \[ y \odot z = 0. \] Now do this again, but this time entrywise multiply the first equality by \(y\) and the second by \(z\); subtract them from each other to deduce \(q \odot (y \odot y - z \odot z) = - \lambda y \odot y - \lambda z \odot z\). We recognize the definition of \(x = \varphi(y, z)\) on the left, and so \[ q \odot x = -\lambda(y\odot y + z\odot z). \] Looking at the two expressions above one coordinate at a time, and recalling that \(x_i = y_i^2 - z_i^2\), we can reason as follows:

• If \(x_i > 0\), then \(y_i \neq 0\). Thus, \(z_i = 0\) and \(q_i x_i = -\lambda y_i^2\). Since \(x_i = y_i^2 > 0\), this simplifies to \(q_i = -\lambda\).
• Likewise, if \(x_i < 0\), then \(q_i = \lambda\).
• If \(x_i = 0\), then \(y_i = z_i = 0\), but this does not reveal anything about \(q_i\).

Consider our target again, as laid out in Lemma 1: the conditions \(x_i \neq 0 \implies \nabla f(x)_i = -\sign(x_i)\lambda\) are already secured by the first two items above.

It remains to show that when \(x_i = 0\) then \(q_i\) belongs to the interval \([-\lambda, \lambda]\). To do so, we invoke the second-order conditions in Lemma 2.

For each \(i\) such that \(x_i = 0\), do as follows. First, let \(\dot y = e_i\) (the \(i\)th column of the identity matrix of size \(n\)) and \(\dot z = 0\). Since \(y_i = z_i = 0\), we see that \(\frac{1}{2}\dot x = y \odot \dot y - z \odot \dot z = 0\). Moreover, \(\dot y \odot \dot y - \dot z \odot \dot z = e_i\) and also \(\|\dot y\|^2 + \|\dot z\|^2 = 1\). Therefore, the second-order conditions reveal that \[ \inner{\nabla f(x)}{e_i} + \lambda \geq 0. \] Second, swap the roles of \(y\) and \(z\) to let \(\dot y = 0\) and \(\dot z = e_i\). We still have \(\dot x = 0\), and so the second-order conditions reveal that \[ \inner{\nabla f(x)}{-e_i} + \lambda \geq 0. \] Combined, we have found that if \(x_i = 0\) then \(\nabla f(x)_i\) is in the interval \([-\lambda, \lambda]\), as desired.

This concludes the proof of Theorem 1.

Numerical illustration

This smooth lift is implemented in the optimization toolbox Manopt (in Matlab) under the name hadamarddifferencelift.

Quoting from the documentation there, here is an illustration with the Lasso problem in Lagrangian form: the aim is to minimize \(f_\lambda(x) = \frac{1}{2}\|Ax - b\|^2 + \lambda\|x\|_1\) in order to recover a sparse \(x \in \Rn\) from \(m < n\) linear measurements.

Since \(f(x) = \frac{1}{2}\|Ax - b\|^2\) is \(C^2\) and convex, we know by Theorem 1 that the function \[ g_\lambda(y, z) = \frac{1}{2} \| A(y \odot y - z \odot z) - b\|^2 + \lambda(\|y\|^2 + \|z\|^2) \] has benign non-convexity: its second-order critical points are globally optimal (“strict saddle property”). Thus, we can minimize it using smooth optimization algorithms without worrying too much about converging to a saddle point.

The Matlab code below requires Manopt (version 8.0+). It allows one to specify \(f\) and its derivatives, and then automatically figures out \(g_\lambda\) and its derivatives (gradient and Hessian).

% Setup random problem data.
% Unknown x_true in R^n is sparse.
% We get m < n linear measurements.
n = 100;
m = 42;
A = randn(m, n);
support_density = .1;
x_true = full(sprandn(n, 1, support_density));
b = A*x_true;

% Describe the quadratic cost function f : R^n -> R.
downstairs.M = euclideanfactory(n, 1);
downstairs.cost = @(x) .5*norm(A*x - b)^2;
downstairs.grad = @(x) A'*(A*x - b);
downstairs.hess = @(x, xdot) A'*A*xdot;

% Select the lift of R^n whose built-in regularizer is the 1-norm.
lift = hadamarddifferencelift(n);

% Call manoptlift with regularization parameter lambda > 0.
lambda = .1;
upstairs = manoptlift(downstairs, lift, [], lambda);

% Minimize g_lambda upstairs.
yz = trustregions(upstairs);

% Map the answer down to a vector in R^n.
x = lift.phi(yz);

% Display the results.
stem(1:n, x_true);
hold all;
stem(1:n, x, '.');
legend('True x', 'Computed x');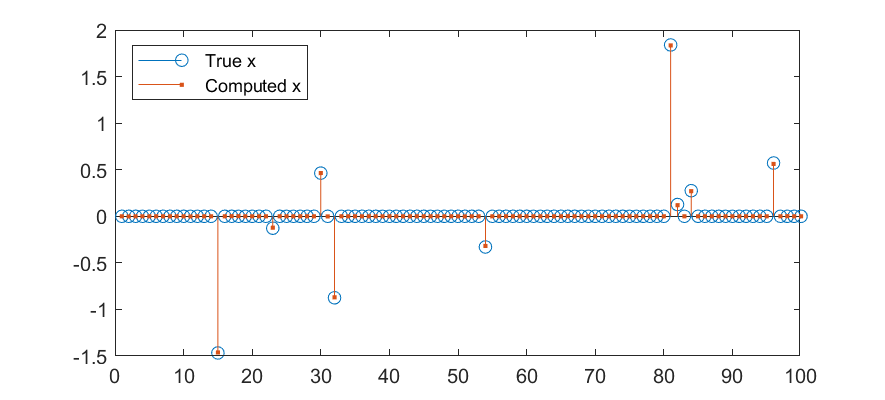

Example of output produced by the illustrative Matlab code solving a Lasso problem.

References

Kolb, C., C. L. Müller, B. Bischl, and D. Rügamer. 2023. “Smoothing the Edges: Smooth Optimization for Sparse Regularization Using Hadamard Overparametrization.” arXiv 2307.03571. https://doi.org/10.48550/arXiv.2307.03571.

Levin, E., J. Kileel, and N. Boumal. 2024. “The Effect of Smooth Parametrizations on Nonconvex Optimization Landscapes.” Mathematical Programming. https://doi.org/10.1007/s10107-024-02058-3.