Gradient descent can converge to any isolated saddle point

Assume \(f \colon \Rn \to \reals\) has \(L\)-Lipschitz continuous gradient (\(f\) is not necessarily \(C^2\)). Pick a point \(x_0 \in \Rn\), and run gradient descent (GD) with constant step-size \(\alpha \in (0, 1/L)\), that is, let \[\begin{align*} x_{k+1} = g(x_k) && \textrm{ with } && g(x) = x - \alpha \nabla f(x). \end{align*}\] Even if the sequence converges to some point \(\bar{x}\), optimizers know not to claim too hastily that this point is a local (let alone global) minimizer of \(f\). Indeed, the limit might be a saddle point of \(f\).

For example, if \(f\) is \(C^2\) and the Hessian \(\nabla^2 f(\bar{x})\) has a positive eigenvalue, then one can use the stable manifold theorem to argue that there exists a whole (local) manifold of initial points \(x_0\) from where GD converges to \(\bar{x}\).

But what if all the eigenvalues of \(\nabla^2 f(\bar{x})\) are non-positive? Then there are no “stable” directions for that saddle point. Could we really converge to it?

Yes.

Theorem 1 Assume \(\bar{x}\) is an isolated critical point of \(f\). If \(\bar{x}\) is not a local maximizer of \(f\), then there exists \(x_0 \neq \bar{x}\) such that gradient descent (as above) initialized at \(x_0\) converges to \(\bar{x}\).

We prove the theorem in the rest of the post, after a brief discussion. Note that one could also assume \(\nabla f\) is merely locally \(L\)-Lipschitz around \(\bar{x}\), as long as we still have \(\alpha < 1/L\).

As a comment: the “if” in the theorem statement is actually an “if and only if”. Intuitively, this is because if GD converges to \(\bar{x}\) then the value of \(f\) along the sequence must gradually decrease down to \(f(\bar{x})\), yet that value is locally maximal. We make this precise at the end of the proof.

Discussion

A version of Theorem 1 for gradient flow (continuous-time setup) appears to be included in (Nowel and Szafraniec 2002, sec. 4). Alternatively, one can also prove it with an adaptation of the argument below. In doing so, sequences become trajectories. As such, a few statements from functional analysis and ODEs come in handy, namely, Grönwall’s inequality, the Arzelà-Ascoli theorem, the Banach-Alaoglu theorem and Mazur’s lemma.

If the critical point is not isolated, then we may not be able to converge to that critical point. The intuition comes from gradient flow. Indeed, it was shown by Palis and de Melo (1982) that trajectories can wind around a limit cycle of minima without converging, even if \(f\) is \(C^\infty\) and the set of minima is a smooth manifold. See also (Absil, Mahony, and Andrews 2005) for discussions related to the discrete-time setup.

Non-isolated critical points can be handled if we make further assumptions on \(f\). For example, with gradient flow, if \(f\) satisfies a Łojasiewicz inequality (e.g., if \(f\) is real-analytic), then one can have convergence to any critical point: see (Moussu 1997, Thm. 3) and Szafraniec (2021). For a proof and consequences that will resonate with optimizers, see the new blog of Chris Criscitiello.

Proof intuition

Since the critical point \(\bar{x}\) is isolated, we can select a Euclidean ball \(B\) of radius \(r > 0\) around \(\bar{x}\) such that \(f\) has no other critical points in that ball. We aim to select a point on (or near) the boundary of that ball such that running GD from there will lead us to \(\bar{x}\).

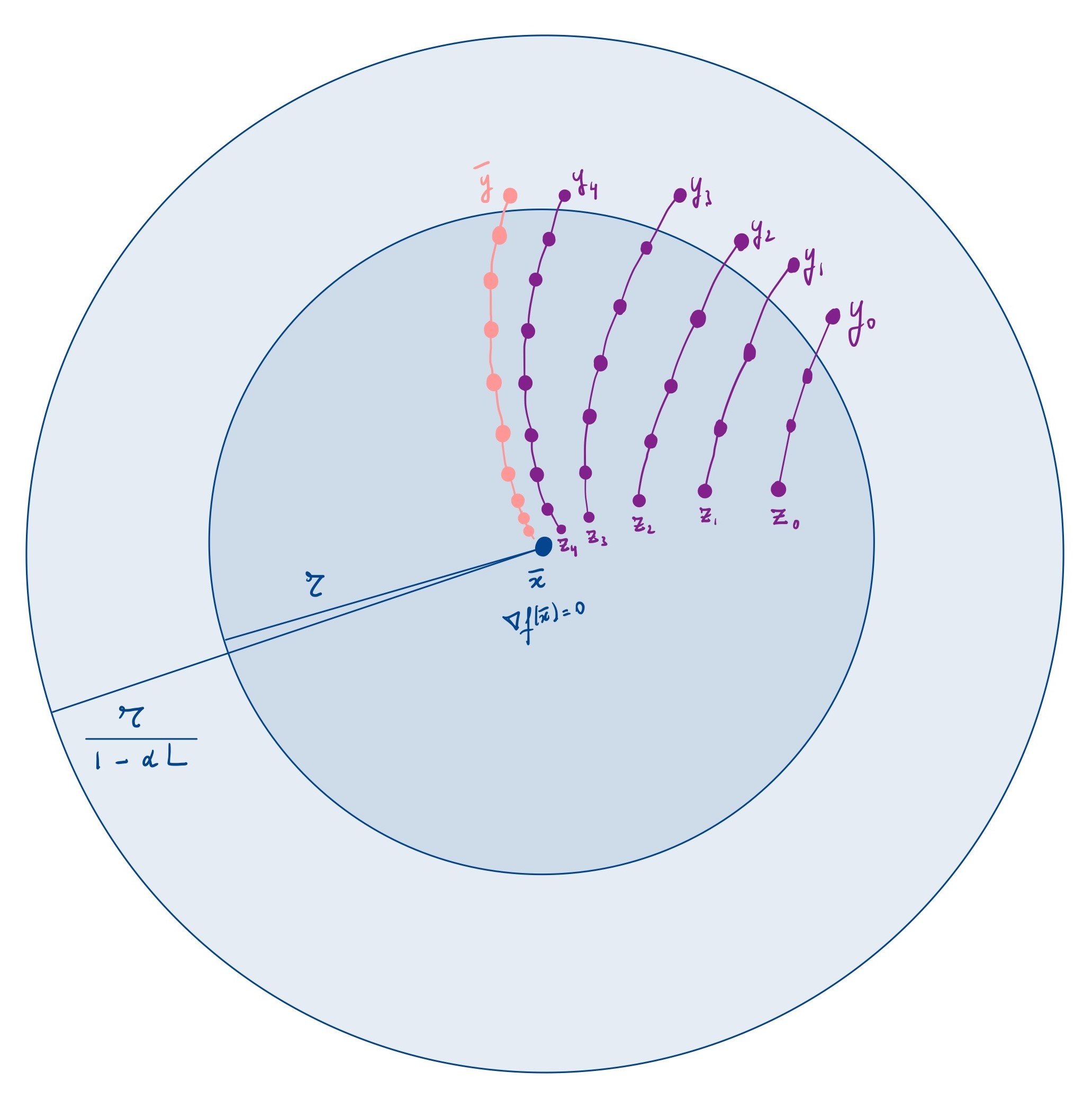
The initial step is to select a sequence of points \(z_k\) that are increasingly close to \(\bar{x}\). This is not a GD sequence, it’s just “a” sequence.

Pick one of these \(z_k\), and run GD in reverse initialized at \(z_k\) (this is valid because gradient steps are invertible, see Lemma 1; note that this is not gradient ascent, it’s just the inverse of a gradient descent step). Two things can happen:

1. Either the sequence never leaves the ball;
2. Or the sequence eventually does leave the ball: let \(y_k\) be the first point with \(\|y_k\| \geq r\).

The first scenario can be excluded simply by choosing the \(z_k\) “higher” than \(\bar{x}\), that is, \(f(z_k) > f(\bar{x})\). (As long as \(\bar{x}\) is not a local maximum, we can do this.) Indeed, if the sequence stays in the ball, it must converge to the only critical point in there, namely, \(\bar{x}\) (see Lemma 4). But also, GD in reverse can only increase the value of \(f\), so it wouldn’t be able to converge to \(\bar{x}\).

Thus, we find that the sequence \(z_0, z_1, \ldots\) provides us with a new sequence \(y_0, y_1, \ldots\), and that starting GD (forward) from each \(y_k\) leads us to the corresponding \(z_k\)—and these get increasingly close to \(\bar{x}\).

From here, it is tempting to consider an accumulation point \(\bar{y}\) for the sequence \((y_k)_{k \geq 0}\). Such a point exists because the \(y_k\) live in a compact set (a ball of radius a bit larger than \(r\), owing to Lemma 2). Intuitively, one might expect that running GD from \(\bar{y}\) could lead us to \(\bar{x}\), and yes, this is so.

To show it, we only need to argue that this GD sequence stays in the ball of radius \(r\) forever. Indeed, it would then have to accumulate in the ball, but it can only accumulate at critical points… and there is only one of those: \(\bar{x}\). (Use Lemma 4 again.)

To argue that the sequence stays in the ball forever, the strategy is to use the fact that the individual GD sequences generated from the points \(y_k\) stay in the ball for longer and longer, and that the “limit sequence” is not so different from the “sequence initialized at the limit”—a swap of two limits, if you will.

Four lemmas about GD

Let \(\|\cdot\|\) denote the usual Euclidean norm on \(\Rn\), and let \[ B(\bar x, r) = \{ x \in \Rn : \|x - \bar x\| \leq r \} \] denote a closed ball of radius \(r\) around \(\bar x\).

Lemma 1 The iteration map \(g \colon \Rn \to \Rn \colon x \mapsto g(x) = x - \alpha \nabla f(x)\) is invertible.

Proof. We proceed as in (Lee et al. 2016, Prop. 8), but without requiring \(f\) to be \(C^2\) (and therefore also without making the stronger claim that \(g\) is a diffeomorphism). Given an arbitrary \(z\), let \(h_z(x) = \frac{1}{2} \|x - z\|^2 - \alpha f(x)\). This function is strongly convex (with constant \(1-\alpha L > 0\) because \(-\alpha f\) has \((\alpha L)\)-Lipschitz gradient). Thus, \(h_z\) has a unique critical point (its unique minimizer). Since \[ \nabla h_z(x) = x - z - \alpha \nabla f(x) = g(x) - z, \] we deduce that the equation \(g(x) = z\) has a unique solution \(x\) for each \(z\), that is, \(g\) is invertible.

The lemma below is useful several times, mainly with \(y = \bar{x}\) and using \(g(\bar{x}) = \bar{x}\).

Lemma 2 For all \(x, y\), the following inequalities hold: \[ (1 - \alpha L)\|x - y\| \leq \|g(x) - g(y)\| \leq (1 + \alpha L)\|x - y\|, \qquad(1)\] and \[ \frac{1}{1+\alpha L} \|x - y\| \leq \|g^{-1}(x) - g^{-1}(y)\| \leq \frac{1}{1-\alpha L} \|x - y\|. \qquad(2)\]

Proof. To verify Eq. 1, first use \(g(x) - g(y) = x - y - \alpha(\nabla f(x) - \nabla f(y))\), then use \(\|\nabla f(x) - \nabla f(y)\| \leq L \|x - y\|\) twice. For Eq. 2, replace \(x\) and \(y\) by \(g^{-1}(x)\) and \(g^{-1}(y)\) in Eq. 1.

The accumulation points of gradient descent are critical points of \(f\) (and likewise for GD “in reverse”).

Lemma 3 If \((g^k(x_0))_{k \geq 0}\) accumulates at \(z\), then \(z\) is a critical point of \(f\) and moreover \(f(z) \leq f(x_0)\). Likewise, if \((g^{-k}(x_0))_{k \geq 0}\) accumulates at \(z\), then \(z\) is a critical point of \(f\) and \(f(z) \geq f(x_0)\).

Proof. Define the constant \(c = \left( 1 - \frac{\alpha L}{2} \right) \alpha > 0\). Since \(\nabla f\) is \(L\)-Lipschitz continuous, we have for all \(x\) that \[ f(x) - f(g(x)) \geq c \|\nabla f(x)\|^2 \qquad(3)\] and (by replacing \(x\) with \(g^{-1}(x)\)) \[ f(g^{-1}(x)) - f(x) \geq c \|\nabla f(g^{-1}(x))\|^2. \] For contradiction, assume \(\nabla f(z) \neq 0\). Let \(r = \|\nabla f(z)\|/2L > 0\). Since \(\nabla f\) is \(L\)-Lipschitz continuous, for all \(x\) in the ball \(\bar B(z, r)\) we have \[ \|\nabla f(x)\| \geq \|\nabla f(z)\| - \|\nabla f(z) - \nabla f(x)\| \geq \frac{1}{2}\|\nabla f(z)\|. \] The sequence visits that ball infinitely many times. Each time it does, the value of \(f\) decreases (for the forward trajectory) or increases (for the backward trajectory) along the sequence by at least a fixed, positive amount. Since \(f\) is monotonically decreasing or increasing (respectively) along the whole sequence, it follows that \(f\) goes to \(-\infty\) or \(+\infty\) along the sequence. Yet, \(f\) is both lower and upper bounded in \(\bar B(z, r)\). Hence, the sequence cannot visit the ball infinitely many times: a contradiction.

Lemma 4 Assume the critical point \(\bar{x}\) is isolated, that is, for some \(r > 0\) the ball \(B(\bar{x}, r)\) contains no other critical point of \(f\). If \((g^k(x_0))_{k \geq 0}\) or \((g^{-k}(x_0))_{k \geq 0}\) eventually stays in that ball forever, then that sequence converges to \(\bar{x}\) and moreover \(f(\bar{x}) \leq f(x_0)\) or \(f(\bar{x}) \geq f(x_0)\), respectively.

Proof. The sequence accumulates somewhere in the ball, and the only critical point in the ball is \(\bar{x}\), hence the sequence accumulates at \(\bar{x}\) by Lemma 3. Assume the sequence does not actually converge to \(\bar{x}\). Then, there exists \(\varepsilon \in (0, r)\) such that some subsequence stays \(\varepsilon\) away from \(\bar{x}\). That subsequence lies in the compact set \(\{ x \in \Rn : \varepsilon \leq \|x - \bar x\| \leq r\}\), hence must accumulate in there. Yet, \(f\) has no critical point in that set: a contradiction by Lemma 3.

The proof

Let \(\bar{x}\) be an isolated critical point of \(f\). Assume \(\bar{x}\) is not a local maximum. Thus, we can pick an arbitrary sequence \((z_k)_{k \geq 0}\) in \(B(\bar{x}, r)\backslash\{\bar{x}\}\) convergent to \(\bar{x}\) such that \(f(z_k) > f(\bar{x})\) for all \(k\). (That sequence does not need to be generated by gradient descent.) For each \(k\), invoke Lemma 1 to let \[ y_k = g^{-\ell_k}(z_k) \] where \(\ell_k\) is the smallest positive integer such that \(\|y_k\| \geq r\). In words: run GD in reverse from \(z_k\), and stop at the first point outside the ball of radius \(r\).

If for some \(k\) no such \(\ell_k\) exists, then it would follow that \(g^{-\ell}(z_k)\) stays in \(B(\bar{x}, r)\) for all \(\ell\). Lemma 4 would then imply that this sequence converges to \(\bar{x}\) and that \(f(\bar{x}) \geq f(z_k)\), which is false. Thus, we can proceed assuming each \(\ell_k\) is finite.

Moreover, Lemma 2 provides \[ r \leq \|y_k - \bar{x}\| = \|g^{-\ell_k}(z_k) - g^{-\ell_k}(\bar{x})\| \leq \left( \frac{1}{1 - \alpha L} \right)^{\ell_k} \|z_k - \bar{x}\|. \] Consequently, \(\ell_k \geq \log_{\frac{1}{1 - \alpha L}}\!\left( \frac{r}{\|z_k - \bar{x}\|} \right) \to \infty\). Since \(y_k\) is the first point outside the ball, we also have \(r > \|g(y_k) - g(\bar{x})\| \geq (1 - \alpha L) \|y_k - \bar{x}\|\), and hence \(r \leq \|y_k - \bar{x}\| \leq \frac{r}{1 - \alpha L}\).

Thus, the sequence \((y_k)_{k \geq 0}\) lies in the compact set \(\{ x \in \Rn : r \leq \|x - \bar{x}\| \leq r/(1 - \alpha L) \}\), hence accumulates at some \(\bar y\) in this set. Pass to a subsequence such that \(y_k\) converges to \(\bar y\). Consider running gradient descent initialized at \(\bar y\). Given \(\ell > 0\), using Lemma 2 again, it holds for all \(k\) such that \(\ell_k \geq \ell\) that \[\begin{align*} \|g^\ell(\bar y) - \bar{x}\| & \leq \|g^\ell(\bar y) - g^\ell(y_k)\| + \|g^\ell(y_k) - \bar{x}\| \\ & \leq \left( 1 + \alpha L \right)^\ell \|\bar y - y_k\| + r. \end{align*}\] Since \(\ell_k \to \infty\), we can take \(k \to \infty\) in the inequality above; and since \(y_k \to \bar y\), it follows that \(\|g^\ell(\bar y) - \bar{x}\| \leq r\). This holds for all \(\ell > 0\), that is, GD initialized at \(\bar{y}\) stays in the ball forever. Now use Lemma 4 to conclude the proof of Theorem 1.

For the converse of Theorem 1, we can reason as follows. Assume that \(\bar{x}\) is a local maximum. For contradiction, say there exists \(x_0 \neq \bar{x}\) such that \(g^k(x_0)\) converges to \(\bar{x}\). On the one hand, we have \(f(g^k(x_0)) \leq f(\bar{x})\) for all \(k\) large enough. On the other hand, Lemma 3 implies \(f(\bar{x}) \leq f(g^k(x_0))\) for all \(k\). Thus, \(f(\bar{x}) = f(g^k(x_0))\) for all \(k\) large enough. In particular, for all \(k\) large enough, \(f(g^{k+1}(x_0)) = f(g^k(x_0))\). By Eq. 3, this implies \(\nabla f(g^k(x_0)) = 0\), and hence \(g^k(x_0) = \bar{x}\) (because for \(k\) large enough \(g^k(x_0)\) is in \(B(\bar{x}, r)\) and \(\bar{x}\) is the only critical point in that ball). Since \(g^{-1}(\bar{x}) = \bar{x}\), we find \(x_0 = \bar{x}\): a contradiction.

References

Absil, P. A., R. Mahony, and B. Andrews. 2005. “Convergence of the Iterates of Descent Methods for Analytic Cost Functions.” SIAM Journal on Optimization 16 (2): 531–47. https://doi.org/10.1137/040605266.

Lee, J. D., M. Simchowitz, M. I. Jordan, and B. Recht. 2016. “Gradient Descent Only Converges to Minimizers.” In Conference on Learning Theory, 1246–57. PMLR. https://proceedings.mlr.press/v49/lee16.html.

Moussu, R. 1997. “Sur La Dynamique Des Gradients: Existence de Variétés Invariantes.” Mathematische Annalen 307 (3): 445–60. https://doi.org/10.1007/s002080050043.

Nowel, A., and Z. Szafraniec. 2002. “On Trajectories of Analytic Gradient Vector Fields.” Journal of Differential Equations 184 (1): 215–23. https://doi.org/10.1006/jdeq.2001.4142.

Palis, J., and W. de Melo. 1982. Geometric Theory of Dynamical Systems: An Introduction. Springer US. https://doi.org/10.1007/978-1-4612-5703-5.

Szafraniec, Z. 2021. “On the Stable Set of an Analytic Gradient Flow.” Journal of Mathematical Analysis and Applications 503 (2): 125321. https://doi.org/10.1016/j.jmaa.2021.125321.